The Unit Root of the Matter: Is it Demand or Supply?

John Cochrane responds to my piece on why there is no evidence that the economy is self-correcting with an excellent blog post

on unit roots. John's post raises two issues. The first is descriptive statistics. What is a parsimonious way to describe the time series properties of the unemployment rate? Here we agree. Unemployment is the sum of a persistent component and a transitory component.

The second is economics. How should we interpret the permanent component?

I claim that the permanent component is caused by shifts from one equilibrium to another and that each of these equilibria is associated with a different permanent unemployment rate. I’ll call that the “demand side theory”. (More on the data here and here and my perspective on the theory here and here ).

Modern macroeconomics interprets the permanent component as shifts in the natural rate of unemployment. I’ll call that the “supply side theory”. That theory is widely accepted and, in my view, wrong. As I predicted in the Financial Times back in 2009, "the next [great economic idea] to fall will be the natural rate hypothesis". 

Lets start with the statistics.

In the comments section, (always worth reading beyond the main post) John and I are in complete agreement that unemployment has two components. One is highly persistent, and well approximated by a random walk. The other is stationary.

Here is John

Hi Roger. We’re converging. Yes, there is an interesting low frequency component in unemployment, that might be modeled well in a short sample with a random walk (unit root = random walk plus stationary component). And unit root asymptotics might be a better approximation to finite sample distributions, plus warn of biases like the AR(1) coefficient.

A random walk, as its name suggests, has an equal chance of going up or down. A stationary variable always returns to a constant number. What about a series that is the sum of a random walk and a stationary component? The stationary bit is always pulling the unemployment rate back to something: but that something is not a number, it’s the random walk component. Unemployment is aiming at a moving target.

John has his own unit root tests. In John's words

"Look at the plot" and "think about the units"

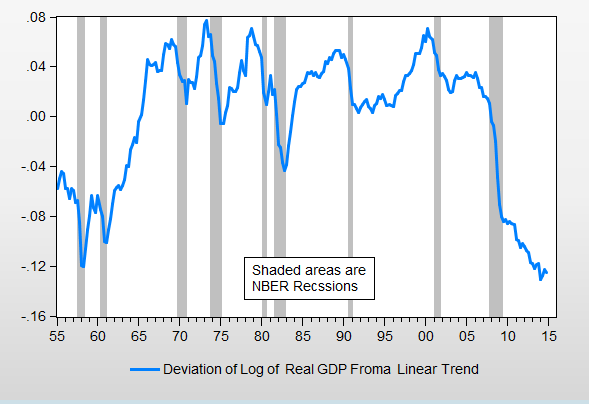
I like that. Here is my “look at the plot” diagram seen through the lens of John’s comment that a unit root equals a “random walk plus stationary component”

John's Unit Root Test: 

"Look at the Plot":

The blue line is the unemployment rate since 1949, the grey shaded areas are the eleven post-war NBER recessions, and the red lines are the means of the unemployment rate for each of the eleven post-war expansions. Because unemployment has a “low frequency component”, the number the economy converges to is different after every recession. It is not a single number. It is a moving target.

So much for the statistics: What about the economics? The central question for policy makers and their academic advisors should be: Why is the target moving? My answer is that aggregate demand, driven by animal spirits, is pulling the economy from one inefficient equilibrium to another. My theoretical work  explains how that idea is consistent with the rest of economic theory. 

The orthodox answer, one we have taught to graduate and undergraduate students alike for the past fifty years is that aggregate supply is shifting from one decade to the next, pushed by changing demographics, shifting tax policies and technological change.  

If permanent movements in the unemployment rate are caused by shifts in aggregate demand, as I believe, we can and should be reacting against these shifts by steering the economy back to the socially optimal unemployment rate. If instead, these movements are caused by shifts in aggregate supply, the moving target is  the socially optimal unemployment rate.

John has not yet staked out a position. On this point he says…

I don't have a definite opinion. There is lots of interesting, new, and unexplored economics on that one. I'll read your paper!

Paul Krugman weighed in on this debate and he claims to agree with John about the statistics, although I’m not sure he read the comments section. 

John and I are in complete agreement: there is  a permanent component in the unemployment rate. That component requires an explanation. Is it demand or is it supply? The answer to that question has huge implications for policy. 

Tired old 1950's theory would attribute the permanent component in unemployment to unavoidable natural rate shifts. Shiny new Neo-Paleo-Keynesian theory would attribute the permanent component to avoidable shifts in animal spirits. Which is it Paul: Demand or Supply?

Beyond 1950's Economic Theory: Nonlinearity, Multiple Equilibria and Sticky Prices

David Glasner has a very nice post on Price Stickiness and Economics with great comments from Rajiv Sethi,  Richard Lipsey and Kevin Donoghue among others. David reacts to a post from Noah Smith: this is all classic stuff

 

Here is David

While I am not hostile to the idea of price stickiness — one of the most popular posts I have written being an attempt to provide a rationale for the stylized (though controversial) fact that wages are stickier than other input, and most output, prices — it does seem to me that there is something ad hoc and superficial about the idea of price stickiness and about many explanations, including those offered by Ball and Mankiw, for price stickiness. I think that the negative reactions that price stickiness elicits from a lot of economists — and not only from Lucas and Williamson — reflect a feeling that price stickiness is not well grounded in any economic theory.

 Let me offer a slightly different criticism of price stickiness as a feature of macroeconomic models, which is simply that although price stickiness is a sufficient condition for inefficient macroeconomic fluctuations, it is not a necessary condition. It is entirely possible that even with highly flexible prices, there would still be inefficient macroeconomic fluctuations. And the reason why price flexibility, by itself, is no guarantee against macroeconomic contractions is that macroeconomic contractions are caused by disequilibrium prices, and disequilibrium prices can prevail regardless of how flexible prices are.

This is my response, first posted as a comment on David's blog,

I have a somewhat different take. I like Lucas’ insistence on equilibrium at every point in time as long as we recognize two facts. 1. There is a continuum of equilibria, both dynamic and steady state and 2. Almost all of them are Pareto suboptimal.

The Arrow-Hahn distaste for RBC models was as much a distaste for the policy implication as it was for the method. At least that’s what I gleaned from conversations with Frank. Perhaps Ken Arrow reads blogs and will jump in and prove me wrong.

David replies...

Roger, I think equilibrium at every point in time is ok if we distinguish between temporary and full equilibrium, but I don’t see how there can be a continuum of full equilibria when agents are making all kinds of long-term commitments by investing in specific capital. Having said that, I certainly agree with you that expectational shifts are very important in determining which equilibrium the economy winds up at. I would certainly be curious to know what Arrow makes of RBC theory, but it would be shocking to me if he had anything positive to say about it. I thought that he always tried to emphasize the ways in which the assumptions of the Arrow-Debreu model deviated from real world conditions.

I agree with much of this. My response to David, which I have also posted on Uneasymoney....

I am comfortable with temporary equilibrium as the guiding principle, as long as the equilibrium in each period is well defined. By that, I mean that, taking expectations as given in each period, each market clears according to some well defined principle. In classical models, that principle is the equality of demand and supply in a Walrasian auction. I do not think that is the right equilibrium concept.

Hicks wanted to separate ‘fix price markets’ from ‘flex price markets’. I don't think that is the right equilibrium concept either. I prefer to use competitive search equilibrium for the labor market. Search equilibrium leads to indeterminacy because there are not enough prices for the inputs to the search process. Classical search theory closes that gap with an arbitrary Nash bargaining weight. I prefer to close it by making expectations fundamental.

Once one treats expectations as fundamental, there is no longer a multiplicity of equilibria. People act in a well defined way and prices clear markets. Of course ‘market clearing’ in a search market may involve unemployment that is considerably higher than the unemployment rate that would be chosen by a social planner. And when there is steady state indeterminacy, as there is in my work, shocks to beliefs may lead the economy to one of a continuum of steady state equilibria.

That brings me to the second part of an equilibrium concept. Are expectations rational in the sense that subjective probability measures over future outcomes coincide with realized probability measures? That is not a property of the real world. It is a consistency property for a model. And yes: if we plop our agents down into a stationary environment, their beliefs should eventually coincide with reality. If the environment changes in an unpredictable way, it is the belief function, a primitive of the model, that guides the economy to a new steady state. And I can envision models where expectations on the transition path are systematically wrong.

The recent ‘nonlinearity debate’ on the blogs confuses the existence of multiple steady states in a dynamic model with the existence of multiple rational expectations equilibria. Nonlinearity is neither necessary nor sufficient for the existence of multiplicity. A linear model can have a unique indeterminate steady state associated with an infinite dimensional continuum of locally stable rational expectations equilibria. A linear model can also have a continuum of attracting points, each of which is an equilibrium. These are not just curiosities. Both of these properties characterize modern dynamic equilibrium models of the real economy.

There are still a number of self-professed Keynesian bloggers out there who see the world through the lens of 1950s theory. They have some catching up to do with the literature.

There is No Evidence that the Economy is Self-Correcting (Very Wonkish)

David Andolfatto asks in a twitter exchange for evidence that deviations of GDP from trend are non-stationary. Here is the raw data. Figure 1 is the residual from a regression of the log of real GDP on a constant and a time trend for quarterly US data from 1955q1 through 2014q4. I will refer to this series as "X".

Figure 1: X = Log of Deviation of Real GDP from Trend

Table 1 reveals the regression of X on itself lagged and on a constant. Remember that these data describe deviations from trend so persistence reflects potentially permanent deviations from the trend growth path. Notice that the coefficient on lagged X is 0.996. That of course, does not establish that the data has a unit root. 

Table 1: Regression Results

There are two approaches to testing formally for a unit root. For one group of tests, for example, the augmented Dickey Fuller test, the null hypothesis is that the series is non-stationary. For a second group, for example the KPSS test, the null hypothesis is that the series is stationary.

Table 2 presents the results of a Dickey Fuller test where the null hypothesis is that X has a unit root. Here we are looking for a test statistic that is small in absolute value if the series has a unit root, reflecting the fact that there is nothing pulling the series back towards trend. 

The null hypothesis that X has a unit root cannot be rejected at the 1%, the 5% or the10% level. 

Table 2: Augmented Dickey Fuller Test

The Dickey Fuller test is known to have very little power over the alternative of a root close to unity and sometimes it helps to look at additional evidence. Table 3 presents the KPSS test for which the null hypothesis is stationarity. Here we are looking for a large test statistic if the series has a unit root.

Table 3: KPSS Test

Notice that here, the null hypothesis of stationarity is overwhelmingly rejected. 

What do we learn from this? Much the same as we learn from the fact that unemployment has a unit root. Just as unemployment can remain persistently high, so GDP can remain persistently below trend. There is no evidence that the economy is self-correcting. 

New Solutions to Old Problems

There was an interesting exchange over the last couple of days between two of my favorite bloggers; Frances Coppola, aka Femina Spectabilis, and Brad DeLong, aka Distinguitur Oeconomicarum. Frances delivered a talk at my alma mater,  Manchester University, on the need to use non-linear models and to recognize the importance of multiple equilibria. Brava! Brad Delong, over at Equitable Growth, takes umbrage at Frances’ charge and rushes to the defense of his former teacher, Olivier Blanchard, aka Nobilis Vir. 

Here is Frances at full tilt

… some of the most influential people in macroeconomics have spent their lives developing theories and models that have been shown to be at best inadequate and at worst dangerously wrong. Olivier Blanchard’s call for policymakers to set policy in such a way that linear models will still work should be seen for what it is – the desperate cry of an aging economist who discovers that the foundations upon which he has built his career are made of sand. He is far from alone.

Perhaps a little harsh. But Frances has a point here Olivier. It's one that was made sometime ago by my emeritus colleague Axel Leijonhufud who referred to what he called corridor effects. Using Axel’s metaphor, Olivier is simply calling for policy makers to keep the economy in the corridor. And who could disagree with that?

Not Brad DeLong for sure, who is supportive of this position. And Brad has a prescription for what it means...

...as long as you can keep the economy on the upward-sloping rather than the flat part of the LM curve, linear models should be good enough for practical purposes. And the government has mighty fiscal policy and credit policy tools at its disposal that it can use to keep high-quality bonds, even short-term bonds, from going to par. 

Quite! The key in this paragraph is the call for policy makers to use  ‘credit policy tools’ in normal times as an additional component of stabilization policy. What might that involve? In my view, central banks and treasuries must recognize their responsibility to counteract the wild swings in asset markets that are the root cause of financial crises.

Horror! Surely, we should leave the allocation of financial capital to those who know best. The decisions of billions of people, freely contracting in markets, can surely make better choices that a cadre of appointed mandarins who purport to understand the economy  better than the markets. Not so. As I argued in the Guardian last year,

The ratio of the stock market price to cyclically adjusted earnings, the PE ratio, is a highly persistent, volatile process. It has been as low as 5 in the 1920s and as high as 45 in the 1990s. When the PE ratio is above its long run average, an investor can profit from selling the market short. When it is below its long run average, a winning strategy is to borrow money and invest it in shares. But although that is sound investment advice in theory, in the real world there is no private investor with a long enough horizon and deep enough pockets to make those trades. As Keynes famously said: "Markets can remain irrational for longer than you can remain solvent."

What can possibly go wrong with private markets? Quoting again from my Guardian op Ed,

Economic theory teaches us that free trade in markets leads to efficient allocations. But a precondition of that doctrine is that everyone who is affected by trade is free to participate in the market. That condition does not hold in the context of the financial markets. We cannot buy insurance over the state of the world into which we are born.

The problem of excess financial volatility is one that cannot be solved by any individual; but it can be solved by government. The Treasury has the power to make commitments on behalf of future generations. The FPC, by exercising that power on behalf of the Treasury, can make trades in the financial markets that capitalise on the inefficient boom-bust financial cycles that are the source of so much human misery. In this way, the FPC will at the same time stabilise volatility in the market and promote financial stability.

There is a growing awareness that free trade in the financial markets does not lead to Pareto efficient outcomes. And, as we have learned only too painfully; pain on Wall Street leads to pain on Main Street. Monetary policy cannot ensure financial stability and stable prices with only one instrument. We must manage the risk composition of the central bank’s balance sheet as well as its size.

Yes David: Unemployment is Sometimes Involuntary

My pal David Andolfatto doesn't like it when I say that some unemployment is involuntary. Here is my response:

David

I am happy with the way you characterize my beliefs in the first paragraph of your blog. Unemployment is clearly not Pareto optimal.  Everything you say after that is at best misleading and at worst dismissive of everything we (at least some of us) learned from Keynes. 

The idea of involuntary unemployment was introduced by Keynes in the General Theory. But you already knew that. It is defined as a situation where (in modern language) the ratio of the marginal disutility of work to the marginal utility of consumption is not equal to the real wage. That seems a pretty accurate description of the equilibrium outcome of labor search models.

Bob Lucas cast a spell over the profession in a series of papers in the 1970s. You are accurately summarizing Bob's view. That view was tied to a three decade long campaign by economists predominately located in Chicago, Minnesota and Rochester (at the time) to discredit Keynesian economics. Tom Sargent reputedly advised his students not to read the General Theory. That was a tragic mistake and we are still suffering from the consequences.

You are right to assert that the important distinction is between equilibria that are Pareto optimal and those that are not. You are wrong to assert that the term 'involuntary unemployment' has no useful meaning. 

I accept your categorization of the allocation of time between three competing ends. Every family, and every member of that family, chooses every day whether they will choose to participate in the labor force. As long as they are in the labor force, they may be employed or unemployed. Those who are unemployed do not choose that state. They must wait for a job offer to appear. In some states, that job offer may take a couple of days to arrive. In others, it may take a couple of years. The activity of waiting for a job, even when it involves active search, can meaningfully be called involuntary unemployment.

The dismissal of 'involuntary unemployment' from the lexicon of the modern economist was introduced as part of a deliberate attack on Keynesian economics. It is time to roll back that attack. As I have shown here, 'involuntary' unemployment is a useful way of distinguishing unemployment that is part of a social optimum, from unemployment that is not.